Kruskal Wallis SAS

Introduction

The Kruskal-Wallis test is a non-parametric equivalent to the one-way ANOVA. For this example, the data used is a subset of R’s datasets::iris, testing for difference in sepal width between species of flower. This data was subset in R and input manually to SAS with a data step.

data iris_sub;
    input Species $ Sepal_Width;
    datalines;
setosa 3.4
setosa 3.0
setosa 3.4
setosa 3.2
setosa 3.5
setosa 3.1
versicolor 2.7
versicolor 2.9
versicolor 2.7
versicolor 2.6
versicolor 2.5
versicolor 2.5
virginica 3.0
virginica 3.0
virginica 3.1
virginica 3.8
virginica 2.7
virginica 3.3
;
run;

Implementing Kruskal-Wallis in SAS

The Kruskal-Wallis test can be implemented in SAS using the NPAR1WAY procedure with WILCOXON option. Below, the test is defined with the indicator variable (Species) by the CLASS statement, and the response variable (Sepal_Width) by the VAR statement. Adding the EXACT statement outputs the exact p-value in addition to the asymptotic result. The null hypothesis is that the samples are from identical populations.

proc npar1way data=iris_sub wilcoxon;
class Species;
var Sepal_Width;
exact;
run;

Results

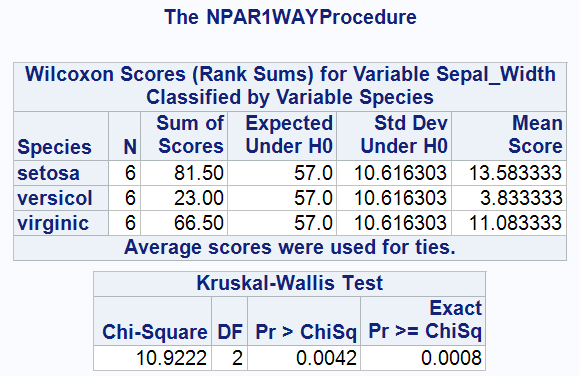
As seen above, SAS outputs a table of Wilcoxon Scores for Sepal_Width by each Species including (per group): the number (N); the sum of scores; the expected sum of scores under the null hypothesis; the standard deviation under the null hypothesis, and the observed mean score. The table also includes a footnote to specify that ties were handled by using the average score.

A table of the test results gives the Kruskal-Wallis rank sum statistic (10.922), the degrees of freedom (2), and the asymptotic p-value of the test (0.0042), and the exact p-value (0.0008). Therefore, the difference in population medians is statistically significant at the 5% level.