data dat_used;
input ID$ ARM$ Y CENS;
cards;
001 A 8.0 1
002 A 8.0 1
003 A 8.0 1
004 A 8.0 1
005 A 8.9 0
006 A 9.5 0
007 A 9.9 0
008 A 10.3 0
009 A 11.0 0
010 A 11.2 0
011 B 8.0 1
012 B 9.2 0
013 B 9.9 0
014 B 10.0 0
015 B 10.6 0
016 B 10.6 0
017 B 11.3 0
018 B 11.8 0
019 B 12.9 0
020 B 13.0 0
;
run;Tobit Regression
Tobit regression
Tobit model
Censoring occurs when data on the dependent variable is only partially known. For example, in virology, sample results could be below the lower limit of detection (eg, 100 copies/mL) and in such a case we only know that the sample result is <100 copies/mL, but we don’t know the exact value.
Let \(y^{*}\) be the the true underlying latent variable, and \(y\) the observed variable. We discuss here censoring on the left:
\[ y = \begin{cases} y^{*}, & y^{*} > \tau \\ \tau, & y^{*} \leq \tau \end{cases} \] We consider tobit regression with a censored normal distribution. The model equation is \[ y_{i}^{*} = X_{i}\beta + \epsilon_{i} \] with \(\epsilon_{i} \sim N(0,\sigma^2)\). But we only observe \(y = max(\tau, y^{*})\). The tobit model uses maximum likelihood estimation (for details see for example Breen, 1996). It is important to note that \(\beta\) estimates the effect of \(x\) on the latent variable \(y^{*}\), and not on the observed value \(y\).
Data used
We assume two equally sized groups (n=10 in each group). The data is censored on the left at a value of \(\tau=8.0\). In group A 4/10 records are censored, and 1/10 in group B.
Example Code using SAS
The analysis will be based on a Tobit analysis of variance with \(Y\), rounded to 1 decimal places, as dependent variable and study group as a fixed covariate. A normally distributed error term will be used. Values will be left censored at the value 8.0.
First a data manipulation step needs to be performed in which the censored values are set to missing for a new variable called lower.
data dat_used;
set dat_used;
if Y <= 8.0 then lower=.; else lower=Y;
run;The data are sorted to make sure the intercept will correspond to the mean of ARM A.
proc sort data=dat_used;
by descending ARM;
run;The LIFEREG procedure is used for tobit regression. The following model syntax is used:
MODEL (lower,upper)= effects / options ;Here, if the lower value is missing, then the upper value is used as a left-censored value.
proc lifereg data=dat_used order=data;
class ARM;
model (lower, Y) = ARM / d=normal;
lsmeans ARM /cl alpha=0.05;
estimate 'Contrast B-A' ARM 1 -1 / alpha=0.05;
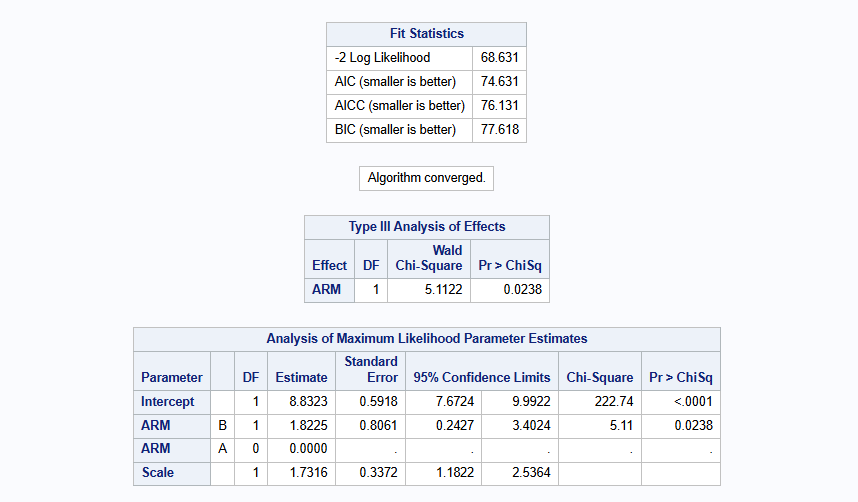
run;The fit statistics, type 3 analysis of effects and parameter estimated are shown here. The output provides an estimate of difference between groups A and B (B-A), namely 1.8225 (se=0.8061). The presented p-value is a two-sided p-value based on the Z-test. The scale parameter is an estimate for \(\sigma\).
The p-value and confidence intervals of the contrast B-A are shown here. The p-value is the same as above.
Reference
Breen, R. (1996). Regression models. SAGE Publications, Inc., https://doi.org/10.4135/9781412985611
Tobin, James (1958). “Estimation of Relationships for Limited Dependent Variables”. Econometrica. 26 (1): 24-36. doi:10.2307/1907382