R vs SAS Linear Models

R vs. SAS ANOVA

Introduction

This section compares the implementation of analysis of variance (ANOVA) in R and SAS. ANOVA compares the mean of two or more groups to determine if at least one group is significantly different from the others.

R and SAS give the same result for the linear model. But, there some differences with calculating sums of squares. If you are looking for type I sum of square that is available in base R stats package using the anova() function. Type II and Type III sum of squares are available in the car and the rstatix packages. rstatix uses the car package to calculate the sum of square, but can be considered easier to use as it handles the contrast for type III automatically.

General Comparison Table

The following table provides an overview of the support and results comparability between R and SAS for the new analysis point.

Analysis Supported in R Supported in SAS Results Match Notes
ANOVA Yes ✅ Yes ✅ Mostly yes R can’t calculate type IV Sum of Squares

Matching Contrasts: R and SAS

Scenario 1: Basic Functionality

R Code Example

In order to get the ANOVA model fit and sum of squares you can use the anova function in the stats package.

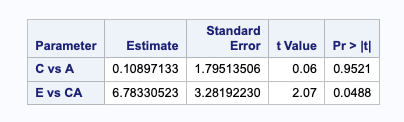
library(emmeans)
Welcome to emmeans.
Caution: You lose important information if you filter this package's results.
See '? untidy'
drug_trial <- read.csv("../data/drug_trial.csv")

lm_model <- lm(formula = post ~ pre + drug, data = drug_trial)
lm_model |>
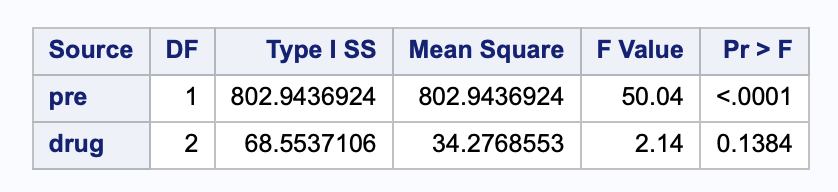
  anova()
Analysis of Variance Table

Response: post
          Df Sum Sq Mean Sq F value    Pr(>F)    
pre        1 802.94  802.94 50.0393 1.639e-07 ***
drug       2  68.55   34.28  2.1361    0.1384    
Residuals 26 417.20   16.05                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

It is recommended to use the emmeans package to get the contrasts between R.

lm_model |>
  emmeans("drug") |>
  contrast(
    method = list(
      "C vs A" = c(-1, 1, 0),
      "E vs CA" = c(-1, -1, 2)
    )
  )
 contrast estimate   SE df t.ratio p.value
 C vs A      0.109 1.80 26   0.061  0.9521
 E vs CA     6.783 3.28 26   2.067  0.0488

In SAS, all contrasts must be manually defined, but the syntax is largely similar in both.

proc glm data=work.mycsv;
   class drug;
   model post = pre drug / solution;
   estimate 'C vs A'  drug -1  1 0;
   estimate 'E vs CA' drug -1 -1 2;
run;

Results Comparison

Provided below is a detailed comparison of the results obtained from both SAS and R.

Sums of Squares
Statistic R Result SAS Result Match
Sum of Square (Type I)

802.94

68.55

802.94

68.55

 Yes
Degrees of Freedom

1

2

1

2

 Yes
Mean Square

802.94

34.28

802.94

34.28

 Yes
F Value

50.04

2.14

50.04

2.14

 Yes
p-value

<0.0001

0.1384

<0.0001

0.1384

 Yes
Contrasts
Statistic R Result SAS Result Match
contrast estimate C vs A 0.109 0.109 Yes
SE 1.80 1.80 Yes
t-ratio 0.06 0.06 Yes
p-value 0.9521 0.9521 Yes
contrast estimate E vs CA 6.783 6.783 Yes
SE 3.28 3.28 Yes
t-ratio 2.07 2.07 Yes
p-value 0.0488 0.0488 Yes

Note, however, that there are some cases where the scale of the parameter estimates between SAS and R is off, though the test statistics and p-values are identical. In these cases, we can adjust the SAS code to include a divisor. As far as we can tell, this difference only occurs when using the predefined Base R contrast methods like contr.helmert.

proc glm data=work.mycsv;
   class drug;
   model post = pre drug / solution;
   estimate 'C vs A'  drug -1  1 0 / divisor = 2;
   estimate 'E vs CA' drug -1 -1 2 / divisor = 6;
run;

Summary and Recommendation

There were no major differences between the R emmeans package and the SAS PROC GLM step in conducting ANOVA on the clinical trial data. Both are robust software tools that generate mostly same results. Scaling for parameter coefficients need to be handled with care however as contrast estimates between R and S differed by a sign.

Additional References

Provide references and additional reading materials for both R and SAS documentation related to the analysis.

R Documentation:

SAS Documentation: