R vs SAS MMRM

Introduction

In this vignette we briefly compare the mmrm::mmrm, SAS’s PROC GLIMMIX, nlme::gls, lme4::lmer, and glmmTMB::glmmTMB functions for fitting mixed models for repeated measures (MMRMs). A primary difference in these implementations lies in the covariance structures that are supported “out of the box”. In particular, PROC GLIMMIX and mmrm are the only procedures which provide support for many of the most common MMRM covariance structures. Most covariance structures can be implemented in gls, though users are required to define them manually. lmer and glmmTMB are more limited. We find that mmmrm converges more quickly than other R implementations while also producing estimates that are virtually identical to PROC GLIMMIX’s.

Datasets

Two datasets are used to illustrate model fitting with the mmrm, lme4, nlme, glmmTMB R packages as well as PROC GLIMMIX. These data are also used to compare these implementations’ operating characteristics.

FEV Data

The FEV dataset contains measurements of FEV1 (forced expired volume in one second), a measure of how quickly the lungs can be emptied. Low levels of FEV1 may indicate chronic obstructive pulmonary disease (COPD). It is summarized below.

                                      Stratified by ARMCD
                               Overall       PBO           TRT
  n                              800           420           380
  USUBJID (%)
     PT[1-200]                   200           105 (52.5)     95 (47.5)
  AVISIT
     VIS1                        200           105            95
     VIS2                        200           105            95
     VIS3                        200           105            95
     VIS4                        200           105            95
  RACE (%)
     Asian                       280 (35.0)    152 (36.2)    128 (33.7)
     Black or African American   300 (37.5)    184 (43.8)    116 (30.5)
     White                       220 (27.5)     84 (20.0)    136 (35.8)
  SEX = Female (%)               424 (53.0)    220 (52.4)    204 (53.7)
  FEV1_BL (mean (SD))          40.19 (9.12)  40.46 (8.84)  39.90 (9.42)
  FEV1 (mean (SD))             42.30 (9.32)  40.24 (8.67)  44.45 (9.51)
  WEIGHT (mean (SD))            0.52 (0.23)   0.52 (0.23)   0.51 (0.23)
  VISITN (mean (SD))            2.50 (1.12)   2.50 (1.12)   2.50 (1.12)
  VISITN2 (mean (SD))          -0.02 (1.03)   0.01 (1.07)  -0.04 (0.98)

BCVA Data

The BCVA dataset contains data from a randomized longitudinal ophthalmology trial evaluating the change in baseline corrected visual acuity (BCVA) over the course of 10 visits. BCVA corresponds to the number of letters read from a visual acuity chart. A summary of the data is given below:

                                      Stratified by ARMCD
                               Overall         CTL            TRT
  n                             8605          4123           4482
  USUBJID (%)
     PT[1-1000]                 1000           494 (49.4)     506 (50.6)
  AVISIT
     VIS1                        983           482            501
     VIS2                        980           481            499
     VIS3                        960           471            489
     VIS4                        946           458            488
     VIS5                        925           454            471
     VIS6                        868           410            458
     VIS7                        816           388            428
     VIS8                        791           371            420
     VIS9                        719           327            392
     VIS10                       617           281            336
  RACE (%)
     Asian                       297 (29.7)    151 (30.6)     146 (28.9)
     Black or African American   317 (31.7)    149 (30.1)     168 (33.2)
     White                       386 (38.6)    194 (39.3)     192 (37.9)
  BCVA_BL (mean (SD))          75.12 (9.93)  74.90 (9.76)   75.40 (10.1)
  BCVA_CHG (mean (SD))
     VIS1                       5.59 (1.31)   5.32 (1.23)    5.86 (1.33)
     VIS10                      9.18 (2.91)   7.49 (2.58)   10.60 (2.36)

Model Implementations

Listed below are some of the most commonly used covariance structures used when fitting MMRMs. We indicate which matrices are available “out of the box” for each implementation considered in this vignette. Note that this table is not exhaustive; PROC GLIMMIX and glmmTMB support additional spatial covariance structures.

Covariance structures	`mmrm`	`PROC GLIMMIX`	`gls`	`lmer`	`glmmTMB`
Ante-dependence (heterogeneous)	X	X
Ante-dependence (homogeneous)	X
Auto-regressive (heterogeneous)	X	X	X
Auto-regressive (homogeneous)	X	X	X		X
Compound symmetry (heterogeneous)	X	X	X		X
Compound symmetry (homogeneous)	X	X	X
Spatial exponential	X	X	X		X
Toeplitz (heterogeneous)	X	X			X
Toeplitz (homogeneous)	X	X
Unstructured	X	X	X	X	X

Code for fitting MMRMs to the FEV data using each of the considered functions and covariance structures are provided below. Fixed effects for the visit number, treatment assignment and the interaction between the two are modeled.

Ante-dependence (heterogeneous)

`PROC GLIMMIX`

PROC GLIMMIX DATA = fev_data;
CLASS AVISIT(ref = 'VIS1') ARMCD(ref = 'PBO') USUBJID;
MODEL FEV1 = AVISIT|ARMCD / ddfm=satterthwaite solution chisq;
RANDOM AVISIT / subject=USUBJID type=ANTE(1);

`mmrm`

mmrm(
  formula = FEV1 ~ ARMCD * AVISIT + adh(VISITN | USUBJID),
  data = fev_data
)

Ante-dependence (homogeneous)

`mmrm`

mmrm(
  formula =FEV1 ~ ARMCD * AVISIT + ad(VISITN | USUBJID),
  data = fev_data
)

Auto-regressive (heterogeneous)

`PROC GLIMMIX`

PROC GLIMMIX DATA = fev_data;
CLASS AVISIT(ref = 'VIS1') ARMCD(ref = 'PBO') USUBJID;
MODEL FEV1 = AVISIT|ARMCD / ddfm=satterthwaite solution chisq;
RANDOM AVISIT / subject=USUBJID type=ARH(1);

`mmrm`

mmrm(
  formula = FEV1 ~ ARMCD * AVISIT + ar1h(VISITN | USUBJID),
  data = fev_data
)

`gls`

gls(
  formula = FEV1 ~ ARMCD * AVISIT,
  data = fev_data,
  correlation = corCAR1(form = ~AVISIT | USUBJID),
  weights = varIdent(form = ~1|AVISIT),
  na.action = na.omit
)

Auto-regressive (homogeneous)

`PROC GLIMMIX`

PROC GLIMMIX DATA = fev_data;
CLASS AVISIT(ref = 'VIS1') ARMCD(ref = 'PBO') USUBJID;
MODEL FEV1 =  ARMCD|AVISIT / ddfm=satterthwaite solution chisq;
RANDOM AVISIT / subject=USUBJID type=AR(1);

`mmrm`

mmrm(
  formula = FEV1 ~ ARMCD * AVISIT + ar1(VISITN | USUBJID),
  data = fev_data
)

`gls`

gls(
  formula = FEV1 ~ ARMCD * AVISIT,
  data = fev_data,
  correlation = corCAR1(form = ~AVISIT | USUBJID),
  na.action = na.omit
)

`glmmTMB`

glmmTMB(
  FEV1 ~ ARMCD * AVISIT + ar1(0 + AVISIT | USUBJID),
  dispformula = ~ 0,
  data = fev_data
)

Compound symmetry (heterogeneous)

`PROC GLIMMIX`

PROC GLIMMIX DATA = fev_data;
CLASS AVISIT(ref = 'VIS1') ARMCD(ref = 'PBO') USUBJID;
MODEL FEV1 = AVISIT|ARMCD / ddfm=satterthwaite solution chisq;
RANDOM AVISIT / subject=USUBJID type=CSH;

`mmrm`

mmrm(
  formula = FEV1 ~ ARMCD * AVISIT + csh(VISITN | USUBJID),
  data = fev_data
)

`gls`

gls(
  formula = FEV1 ~ ARMCD * AVISIT,
  data = fev_data,
  correlation = corCompSymm(form = ~AVISIT | USUBJID),
  weights = varIdent(form = ~1|AVISIT),
  na.action = na.omit
)

`glmmTMB`

glmmTMB(
  FEV1 ~ ARMCD * AVISIT + cs(0 + AVISIT | USUBJID),
  dispformula = ~ 0,
  data = fev_data
)

Compound symmetry (homogeneous)

`PROC GLIMMIX`

PROC GLIMMIX DATA = fev_data;
CLASS AVISIT(ref = 'VIS1') ARMCD(ref = 'PBO') USUBJID;
MODEL FEV1 = AVISIT|ARMCD / ddfm=satterthwaite solution chisq;
RANDOM AVISIT / subject=USUBJID type=CS;

`mmrm`

mmrm(
  formula = FEV1 ~ ARMCD * AVISIT + cs(VISITN | USUBJID),
  data = fev_data
)

`gls`

gls(
  formula = FEV1 ~ ARMCD * AVISIT,
  data = fev_data,
  correlation = corCompSymm(form = ~AVISIT | USUBJID),
  na.action = na.omit
)

Spatial exponential

`PROC GLIMMIX`

PROC GLIMMIX DATA = fev_data;
CLASS AVISIT(ref = 'VIS1') ARMCD(ref = 'PBO') USUBJID;
MODEL FEV1 = AVISIT|ARMCD / ddfm=satterthwaite solution chisq;
RANDOM / subject=USUBJID type=sp(exp)(visitn) rcorr;

`mmrm`

mmrm(
  formula = FEV1 ~ ARMCD * AVISIT + sp_exp(VISITN | USUBJID),
  data = fev_data
)

`gls`

gls(
  formula = FEV1 ~ ARMCD * AVISIT,
  data = fev_data,
  correlation = corExp(form = ~AVISIT | USUBJID),
  weights = varIdent(form = ~1|AVISIT),
  na.action = na.omit
)

`glmmTMB`

# NOTE: requires use of coordinates
glmmTMB(
  FEV1 ~ ARMCD * AVISIT + exp(0 + AVISIT | USUBJID),
  dispformula = ~ 0,
  data = fev_data
)

Toeplitz (heterogeneous)

`PROC GLIMMIX`

PROC GLIMMIX DATA = fev_data;
CLASS AVISIT(ref = 'VIS1') ARMCD(ref = 'PBO') USUBJID;
MODEL FEV1 = AVISIT|ARMCD / ddfm=satterthwaite solution chisq;
RANDOM AVISIT / subject=USUBJID type=TOEPH;

`mmrm`

mmrm(
  formula = FEV1 ~ ARMCD * AVISIT + toeph(AVISIT | USUBJID),
  data = fev_data
)

`glmmTMB`

 glmmTMB(
  FEV1 ~ ARMCD * AVISIT + toep(0 + AVISIT | USUBJID),
  dispformula = ~ 0,
  data = fev_data
)

Toeplitz (homogeneous)

`PROC GLIMMIX`

PROC GLIMMIX DATA = fev_data;
CLASS AVISIT(ref = 'VIS1') ARMCD(ref = 'PBO') USUBJID;
MODEL FEV1 = AVISIT|ARMCD / ddfm=satterthwaite solution chisq;
RANDOM AVISIT / subject=USUBJID type=TOEP;

`mmrm`

mmrm(
  formula = FEV1 ~ ARMCD * AVISIT + toep(AVISIT | USUBJID),
  data = fev_data
)

Unstructured

`PROC GLIMMIX`

PROC GLIMMIX DATA = fev_data;
CLASS AVISIT(ref = 'VIS1') ARMCD(ref = 'PBO') USUBJID;
MODEL FEV1 = ARMCD|AVISIT / ddfm=satterthwaite solution chisq;
RANDOM AVISIT / subject=USUBJID type=un;

`mmrm`

mmrm(
  formula = FEV1 ~ ARMCD * AVISIT + us(AVISIT | USUBJID),
  data = fev_data
)

`gls`

gls(
  formula = FEV1 ~  ARMCD * AVISIT,
  data = fev_data,
  correlation = corSymm(form = ~AVISIT | USUBJID),
  weights = varIdent(form = ~1|AVISIT),
  na.action = na.omit
)

`lmer`

lmer(
  FEV1 ~ ARMCD * AVISIT + (0 + AVISIT | USUBJID),
  data = fev_data,
  control = lmerControl(check.nobs.vs.nRE = "ignore"),
  na.action = na.omit
)

`glmmTMB`

glmmTMB(
  FEV1 ~ ARMCD * AVISIT + us(0 + AVISIT | USUBJID),
  dispformula = ~ 0,
  data = fev_data
)

Benchmarking

Next, the MMRM fitting procedures are compared using the FEV and BCVA datasets. FEV1 measurements are modeled as a function of race, treatment arm, visit number, and the interaction between the treatment arm and the visit number. Change in BCVA is assumed to be a function of race, baseline BCVA, treatment arm, visit number, and the treatment–visit interaction. In both datasets, repeated measures are modeled using an unstructured covariance matrix. The implementations’ convergence times are evaluated first, followed by a comparison of their estimates. Finally, we fit these procedures on simulated BCVA-like data to assess the impact of missingness on convergence rates.

Convergence Times

FEV Data

The mmrm, PROC GLIMMIX, gls, lmer, and glmmTMB functions are applied to the FEV dataset 10 times. The convergence times are recorded for each replicate and are reported in the table below.

Comparison of convergence times: milliseconds
Implementation	Median	First Quartile	Third Quartile
mmrm	56.15	55.76	56.30
PROC GLIMMIX	100.00	100.00	100.00
lmer	247.02	245.25	257.46
gls	687.63	683.50	692.45
glmmTMB	715.90	708.70	721.57

It is clear from these results that mmrm converges significantly faster than other R functions. Though not demonstrated here, this is generally true regardless of the sample size and covariance structure used. mmrm is faster than PROC GLIMMIX.

BCVA Data

The MMRM implementations are now applied to the BCVA dataset 10 times. The convergence times are presented below.

Comparison of convergence times: seconds
Implementation	Median	First Quartile	Third Quartile
mmrm	3.36	3.32	3.46
glmmTMB	18.65	18.14	18.87
PROC GLIMMIX	36.25	36.17	36.29
gls	164.36	158.61	165.93
lmer	165.26	157.46	166.42

We again find that mmrm produces the fastest convergence times on average.

Marginal Treatment Effect Estimates Comparison

We next estimate the marginal mean treatment effects for each visit in the FEV and BCVA datasets using the MMRM fitting procedures. All R implementations’ estimates are reported relative to PROC GLIMMIX’s estimates. Convergence status is also reported.

FEV Data

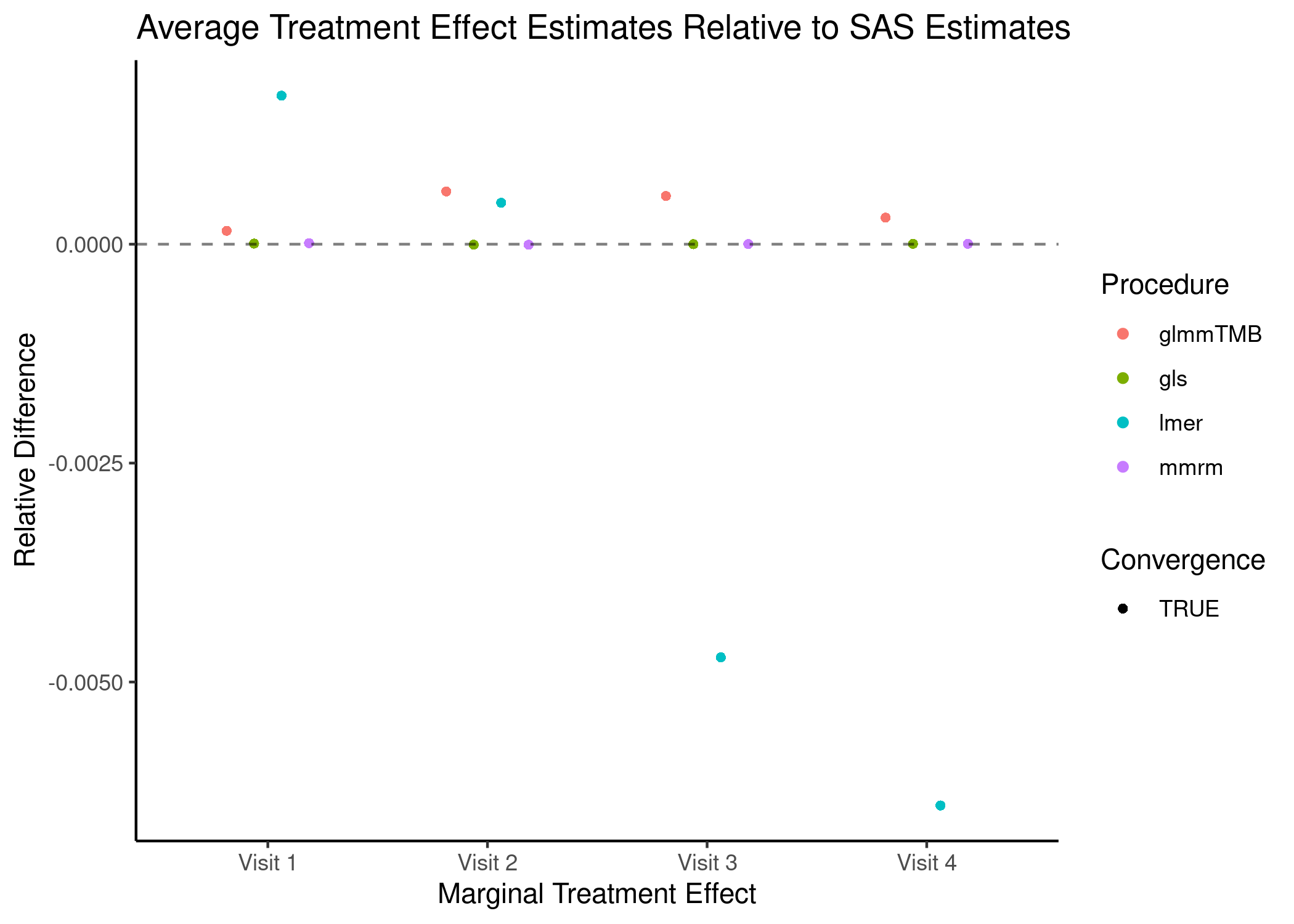
The R procedures’ estimates are very similar to those output by PROC GLIMMIX, though mmrm and gls generate the estimates that are closest to those produced when using SAS. All methods converge using their default optimization arguments.

BCVA Data

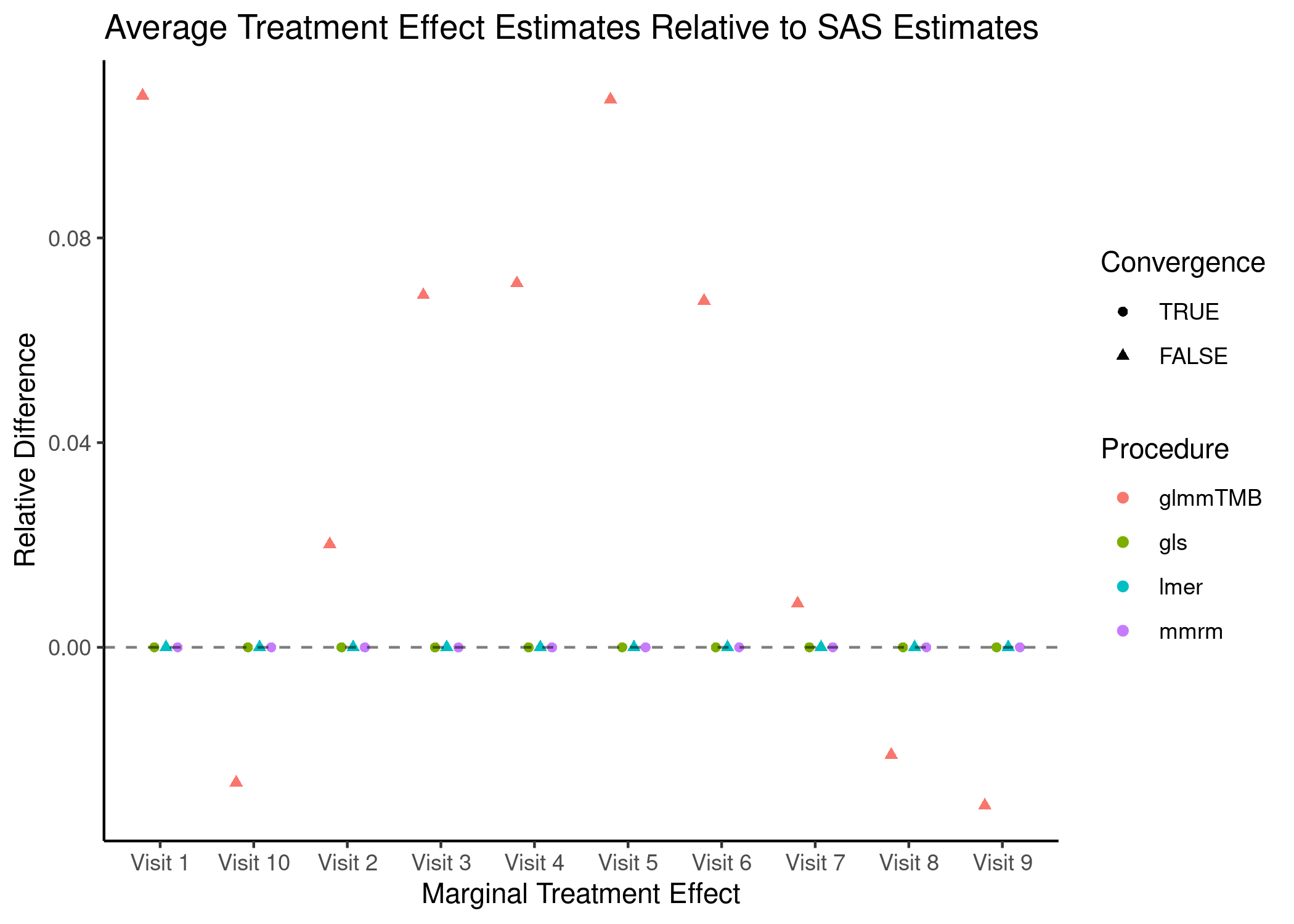
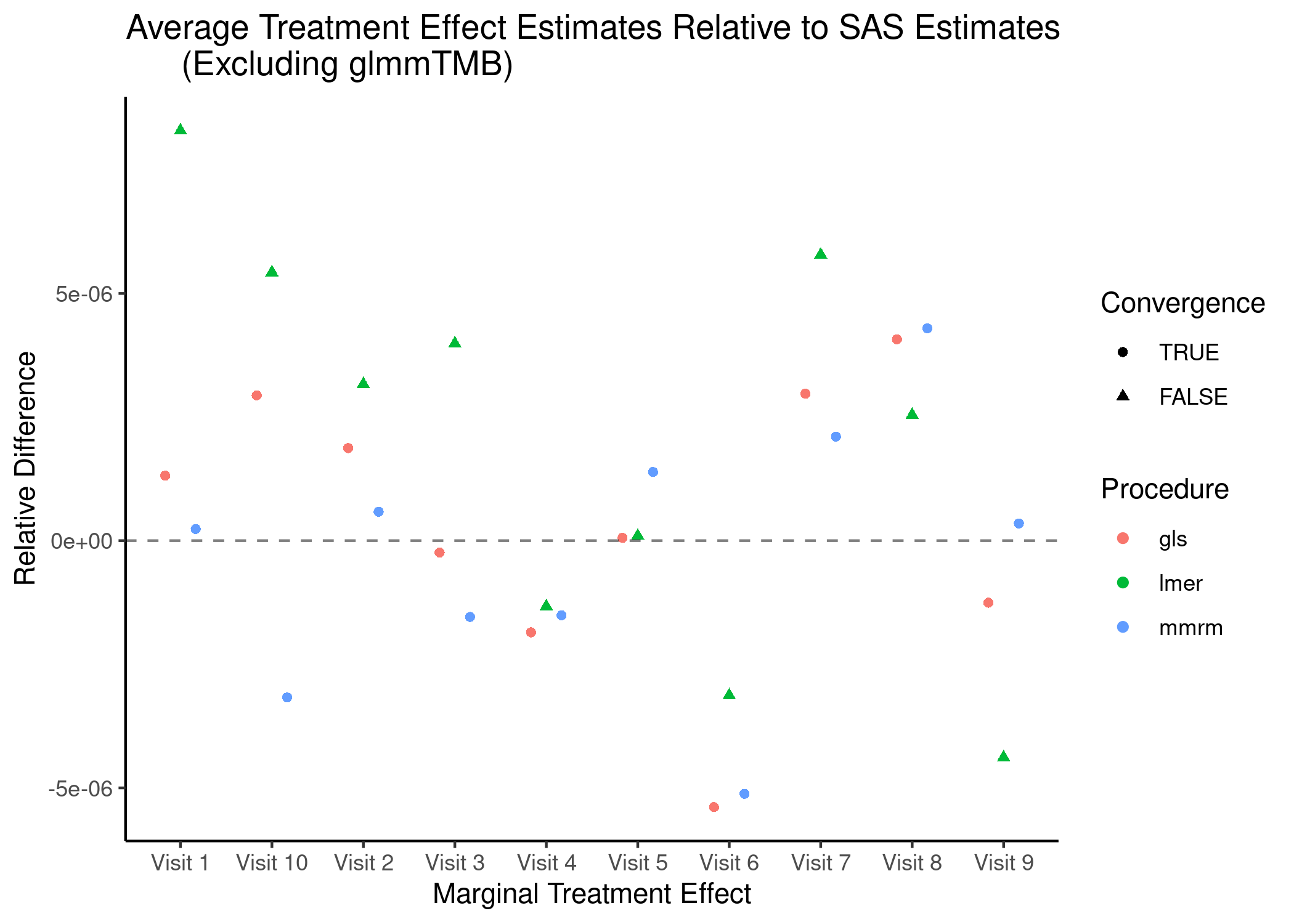
mmrm, gls and lmer produce estimates that are virtually identical to PROC GLIMMIX’s, while glmmTMB does not. This is likely explained by glmmTMB’s failure to converge. Note too that lmer fails to converge.

Impact of Missing Data on Convergence Rates

The results of the previous benchmark suggest that the amount of patients missing from later time points affect certain implementations’ capacity to converge. We investigate this further by simulating data using a data-generating process similar to that of the BCVA datasets, though with various rates of patient dropout.

Ten datasets of 200 patients are generated each of the following levels of missingness: none, mild, moderate, and high. In all scenarios, observations are missing at random. The number patients observed at each visit is obtained for one replicated dataset at each level of missingness is presented in the table below.

Number of patients per visit
	none	mild	moderate	high
VIS01	200	196.7	197.6	188.1
VIS02	200	195.4	194.4	182.4
VIS03	200	195.1	190.7	175.2
VIS04	200	194.1	188.4	162.8
VIS05	200	191.6	182.5	142.7
VIS06	200	188.2	177.3	125.4
VIS07	200	184.6	168.0	105.9
VIS08	200	178.5	155.4	82.6
VIS09	200	175.3	139.9	58.1
VIS10	200	164.1	124.0	39.5

The convergence rates of all implementations for stratified by missingness level is presented in the plot below.

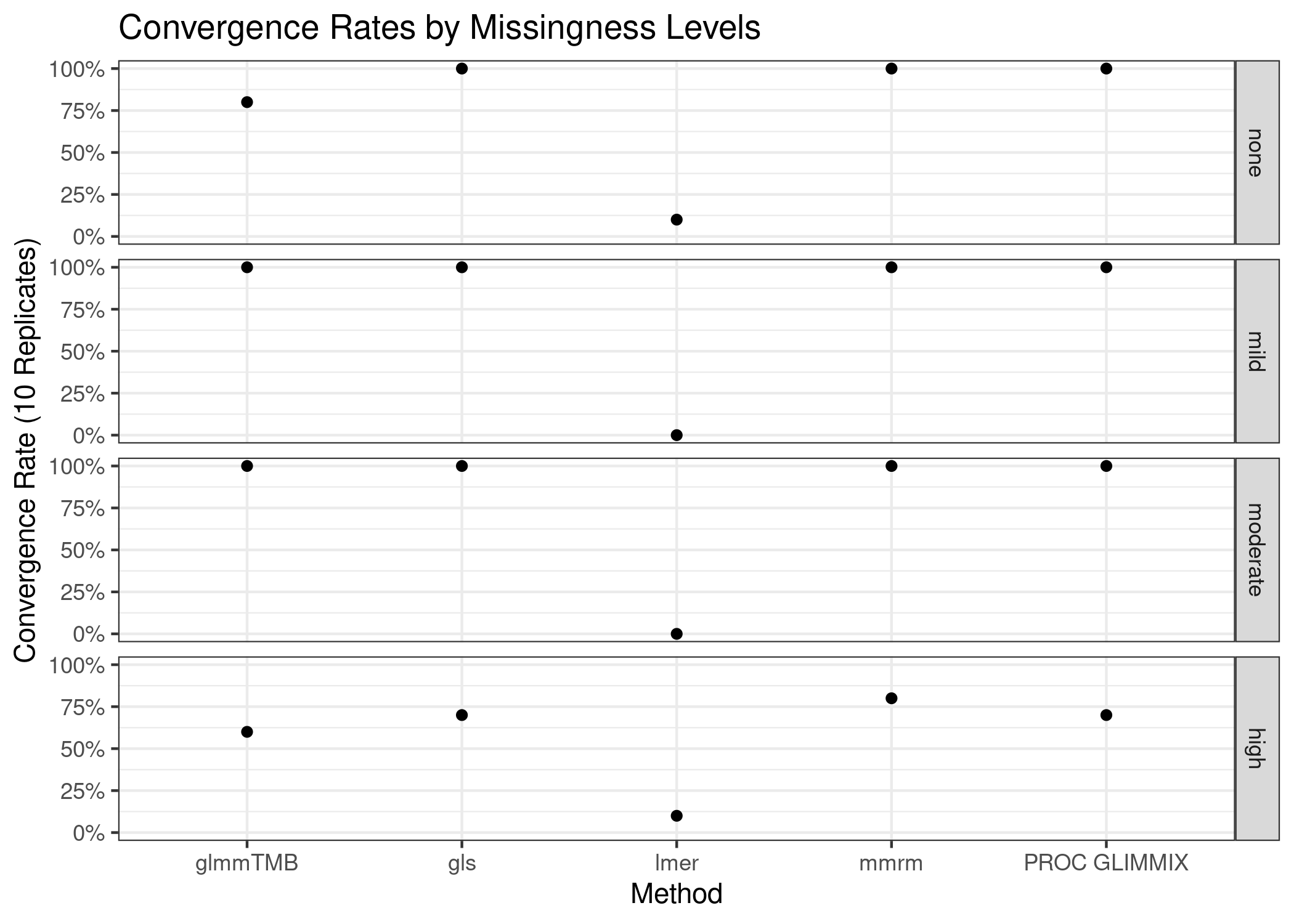
mmrm, gls, and PROC GLIMMIX are resilient to missingness, only exhibiting some convergence problems in the scenarios with the most missingness. These implementations converged in all the other scenarios’ replicates. glmmTMB, on the other hand, has convergence issues in the no-, mild-, and high-missingness datasets, with the worst convergence rate occurring in the datasets with the most dropout. Finally, lmer is unreliable in all scenarios, suggesting that it’s convergence issues stem from something other than the missing observations.

Note that the default optimization schemes are used for each method; these schemes can be modified to potentially improve convergence rates.

A more comprehensive simulation study using data-generating processes similar to the one used here is outlined in the simulations/missing-data-benchmarks subdirectory. In addition to assessing the effect of missing data on software convergence rates, we also evaluate these methods’ fit times and empirical bias, variance, 95% coverage rates, type I error rates and type II error rates. mmrm is found to be the most most robust software for fitting MMRMs in scenarios where a large proportion of patients are missing from the last time points. Additionally, mmrm has the fastest average fit times regardless of the amount of missingness. All implementations considered produce similar empirical biases, variances, 95% coverage rates, type I error rates and type II error rates.