Estimating Cumulative Incidence Functions Using R

Objective

In this document we present how to estimate the cumulative incidence function (CIF) in R. We focus on the competing risks model where each subject experiences only one out of k possible events as depicted in the figure below.

R Packages

We identify three packages:

cmprsk
tidycmprsk
survival

The cmprsk package implements the methods described in Gray (1988) for testing CIFs across different groups. The tidycmprsk package is a wrapper for cmprsk. It uses syntax similar to other survival analysis packages, and returns survival objects. In this document, we illustrate how to use the tidycmprsk package for estimating and testing CIFs. More details and other functionalities can be found here.

The survival package is a general purpose survival analysis package. Its scope is far beyond the competing risks model. We will demonstrate how to estimate the CIFs using this package.

Data used

The bone marrow transplant (BTM) dataset as presented by Guo & So (2018) is used. The dataset has the following variables:

Group has three levels, indicating three disease groups: ALL, AML-Low Risk, AML-High Risk.
T is the disease-free survival time in days. A derived variable TYears = T/365.25 is used in the analysis.
Status has value 0 if T is censored; 1 if T is time to relapse; 2 if T is time to death.
WaitTime is the waiting time to transplant in days. This variable is not used here.
A new variable ID is created.

require(dplyr)
bmt <- haven::read_sas(file.path("../data/bmt.sas7bdat")) %>%
  mutate(
    Group = factor(Group, 
                   levels = c(1, 2, 3), 
                   labels = c('ALL', 'AML-Low Risk', 'AML-High Risk')
    ),
    Status = factor(Status,
                    levels = c(0, 1, 2),
                    labels = c('Censored', 'Relapse', 'Death')),
    TYears = T / 365.25,
    ID = row_number()
  )

Estimating CIFs

The `tidycmprsk` Package

CIF Estimates and Gray’s Test

The tidycmprsk::cuminc() function requires a Surv object. Therefore, the first level of the event status variable (in this example Status) must represent censoring.

require(survival)
require(tidycmprsk)
require(tidyverse)
cif.1 <- cuminc(Surv(TYears, Status) ~ Group, data = bmt)

Gray’s test statistics and p-value:

knitr::kable(
  glance(cif.1) %>% 
  pivot_longer(
    everything(),
    names_to = c(".value", "outcome_id"),
    names_pattern = "(.*)_(.*)"
  )
)

outcome_id	outcome	statistic	df	p.value
1	Relapse	11.9228820	2	0.0025762
2	Death	0.1374108	2	0.9336017

CIF estimates for time to relapse at selected timepoints for ‘AML-Low Risk’ patients:

knitr::kable(
  cif.1 %>% 
  tidy(times = c(0.5, 1, 1.5, 2, 3)) %>%
  select(time, outcome, strata, estimate, std.error, conf.low, conf.high) %>% 
  filter(outcome == 'Relapse' & strata == 'AML-Low Risk') %>%
  mutate(time = as.character(time),
         across(where(is.numeric), ~ num(., digits = 4))
  )
)

time	outcome	strata	estimate	std.error	conf.low	conf.high
0.5	Relapse	AML-Low Risk	0.0000	0.0000	NA	NA
1	Relapse	AML-Low Risk	0.0741	0.0360	0.0234	0.1646
1.5	Relapse	AML-Low Risk	0.1296	0.0463	0.0563	0.2344
2	Relapse	AML-Low Risk	0.1481	0.0489	0.0685	0.2565
3	Relapse	AML-Low Risk	0.1667	0.0514	0.0813	0.2783

Two points to note:

The current version of cmprsk, and hence tidycmprsk, estimates the variance of the CIF estimates asymptotically as in Aalen (1978). There is no option to change it to other methods.
tidycmprsk::cuminc() offers pointwise CIs for the CIF estimates using the log-log transforms. There is no other options.

CIF Plots

require(ggsurvfit)
cif.1 %>%
  ggcuminc(outcome = 'Death') +
  ## add_confidence_interval() +
  add_risktable() +
  xlab('Time (years) to death')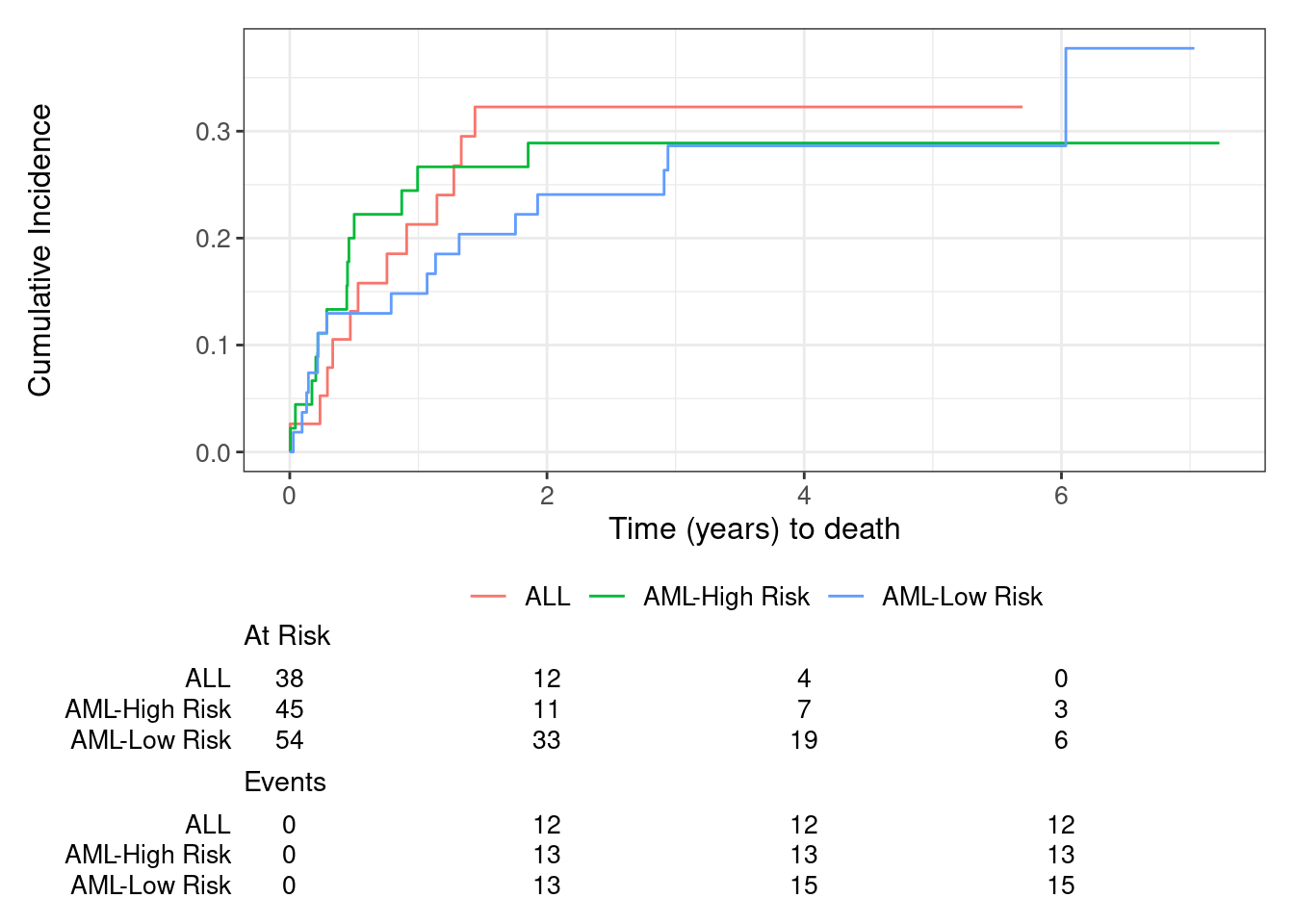

cif.1 %>%
  ggcuminc(outcome = 'Relapse') +
  ## add_confidence_interval() +
  add_risktable() +
  xlab('Time (years) to relapse')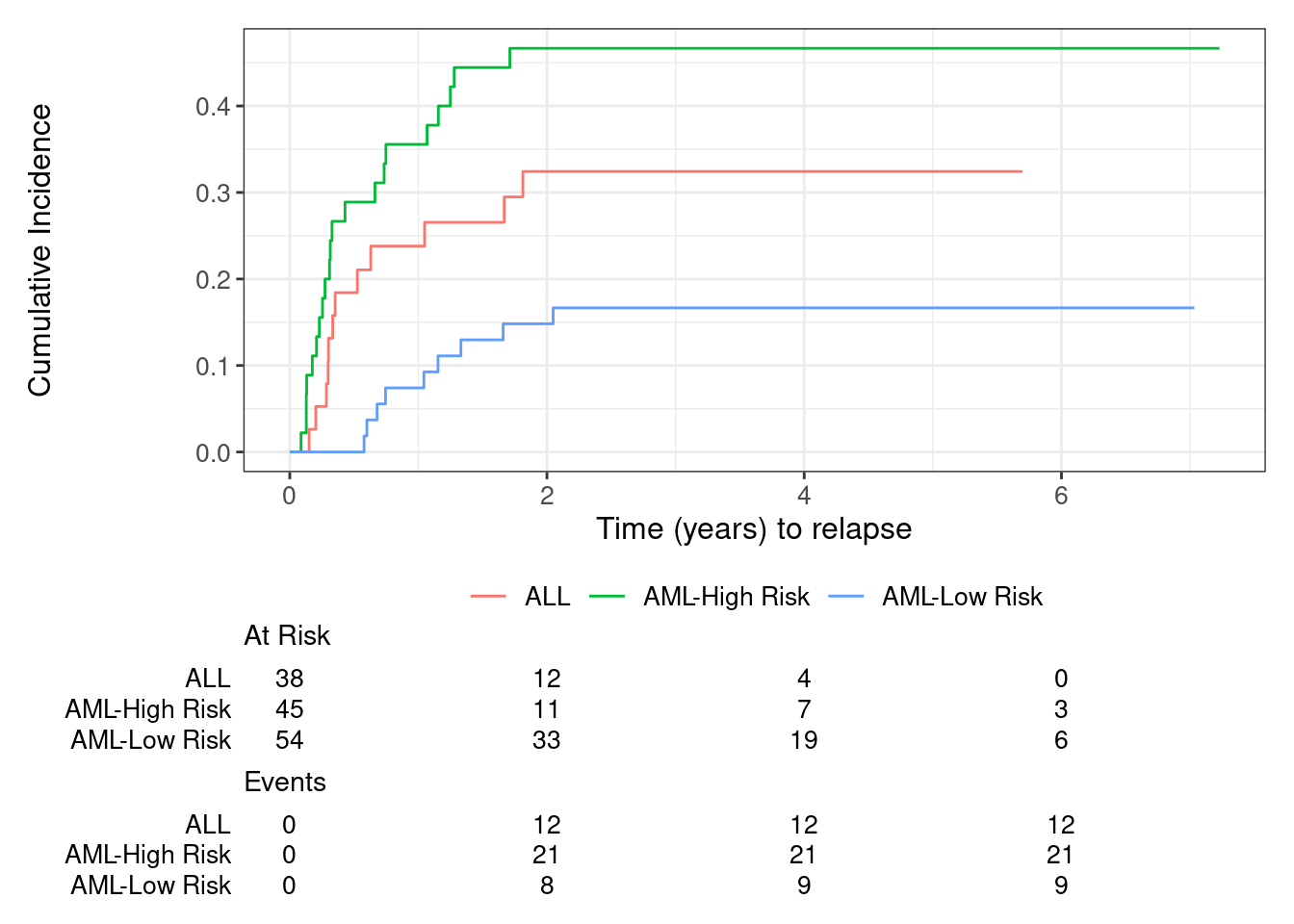

The `survival` Package

CIF Estimates

Using the bone marrow transplant example, the following code shows how to estimate the CIF for time to relapse or to death:

cif.2 <- survfit(Surv(TYears, Status) ~ Group,
                 data = bmt,
                 se.fit = TRUE,
                 conf.type = 'log-log', ## default is 'log'
                 id = ID,
                 robust = TRUE ## default for multi-state model
                 )
## summary(cif.2)

A few points to note:

survfit() returns the probability of being in a state (pstate). The CIF is its complement, i.e., CIF = 1 - pstate.
Gray’s test for testing equality across groups is not performed.
In this example survfit() recognizes that the input are in multi-state model format; therefore, it estimates the variances of the CIFs with an infinitesimal jackknife (see Therneau (2024)). The CIs, as a result, are different from that estimated based on Aalen’s or the delta method as done in SAS PROC LIFETEST.
The survival package also offers a different syntax for estimating CIFs. Users need to first call finegray() separately for each event to reformat the data, then apply survfit() for each event. The CIF estimates are identical since the same estimation method is used; the variances can be different from directly calling survfit() with data in multi-state model format, since finegray() artificially extends the observed time for the competing events (see Therneau (2024)).

CIF Plots

The same ggcuminc() syntax can be applied to the survfit() output cif.2.

Summary

Both tidycmprsk::cminc() (as inherited from cmprsk::cuminc()) and survival::survfit() implement Aalen-Johansen estimator. For competing risks it reduces to CIF, which has a closed form formulation. The results are identical as produced by SAS PROC LIFETEST.

Certain options in SAS, e.g., the delta method for variance estimation or other types of transformation for calculating the CIs, are not available in the current versions of tidycmprsk::cuminc() or survival::survfit(). However, the outputs from both contain enough information that these options can be manually implemented by users. For example, Pintilie (2006) provides R code for deriving the variances for the estimated CIFs based on the delta method.

Session Info

 #| echo: false
 si <- sessioninfo::session_info(
 c("cmprsk", "tidycmprsk", "survival" ) #Vector of packages used 
 , dependencies = FALSE)
 si

─ Session info ───────────────────────────────────────────────────────────────
 setting  value
 version  R version 4.4.2 (2024-10-31)
 os       Ubuntu 24.04.1 LTS
 system   x86_64, linux-gnu
 ui       X11
 language (EN)
 collate  C.UTF-8
 ctype    C.UTF-8
 tz       UTC
 date     2024-12-16
 pandoc   3.4 @ /opt/quarto/bin/tools/ (via rmarkdown)

─ Packages ───────────────────────────────────────────────────────────────────
 ! package    * version date (UTC) lib source
 P cmprsk       2.2-12  2024-05-19 [?] RSPM (R 4.4.0)
   survival   * 3.7-0   2024-06-05 [2] CRAN (R 4.4.2)
 P tidycmprsk * 1.1.0   2024-08-17 [?] RSPM (R 4.4.0)

 [1] /home/runner/work/CAMIS/CAMIS/renv/library/linux-ubuntu-noble/R-4.4/x86_64-pc-linux-gnu
 [2] /opt/R/4.4.2/lib/R/library

 P ── Loaded and on-disk path mismatch.

──────────────────────────────────────────────────────────────────────────────

Reference

Aalen O. (1978). Nonparametric Estimation of Partial Transition Probabilities in Multiple Decrement Models, Annals of Statistics, 6:534-545.

Gray R. (1988). A Class of K-Sample Tests for Comparing the Cumulative Incidence of a Competing Risk, Annals of Statistics, 16:1141-1154.

Gray R. (2024). cmprsk: Subdistribution Analysis of Competing Risks. R package version 2.2-12. https://cran.r-project.org/web/packages/cmprsk/cmprsk.pdf

Guo C and So Y. (2018). Cause-Specific Analysis of Competing Risks Using the PHREG Procedure. In Proceedings of the SAS Global Forum 2018 Conference. Cary, NC: SAS Institute Inc. https://support.sas.com/resources/papers/proceedings18/2159-2018.pdf.

Pintilie M. (2006). Competing Risks: A Practical Perspective. Wiley.
http://dx.doi.org/10.1002/9780470870709

Sjoberg D and Fei T. (2023). tidycmprsk: Competing Risks Estimation. https://github.com/MSKCC-Epi-Bio/tidycmprsk

Therneau T. (2024). A Package for Survival Analysis in R. R package version 3.7-0, https://CRAN.R-project.org/package=survival.

Objective

R Packages

Data used

Estimating CIFs

The tidycmprsk Package

CIF Estimates and Gray’s Test

CIF Plots

The survival Package

CIF Estimates

CIF Plots

Summary

Reference

The `tidycmprsk` Package

The `survival` Package