data d1;
length trt_grp $ 9;
input trt_grp $ WtGain @@;
datalines;
placebo 94 placebo 12 placebo 26 placebo 89
placebo 88 placebo 96 placebo 85 placebo 130
placebo 75 placebo 54 placebo 112 placebo 69
placebo 104 placebo 95 placebo 53 placebo 21
treatment 45 treatment 62 treatment 96 treatment 128
treatment 120 treatment 99 treatment 28 treatment 50
treatment 109 treatment 115 treatment 39 treatment 96
treatment 87 treatment 100 treatment 76 treatment 80
;
run;Independent Two-Sample t-test
Data Used
The following data was used in this example.
Independent Two-Sample t-test in SAS
The null hypothesis of the Independent Samples t-test is, the means for the two populations are equal.
In SAS the following code was used to test the mean comparison (mean of Weight Gain) of two independent treatment groups (Treatment and Placebo). Both the Student’s t-test and Welch’s t-test (the Satterthwaite approximation is used to calculate the effective degrees of freedom and variance) in the same call.
For this example, we’re testing the significant difference in mean of Weight gain (WtGain) between treatment and placebo (trt_grp) using PROC TTEST procedure in SAS.
proc ttest data=d1;
class trt_grp;
var WtGain;
run; Output:
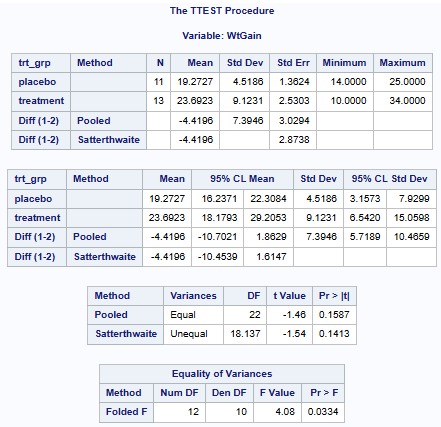
Figure 1: Test results for independent t-test using PROC TTEST in SAS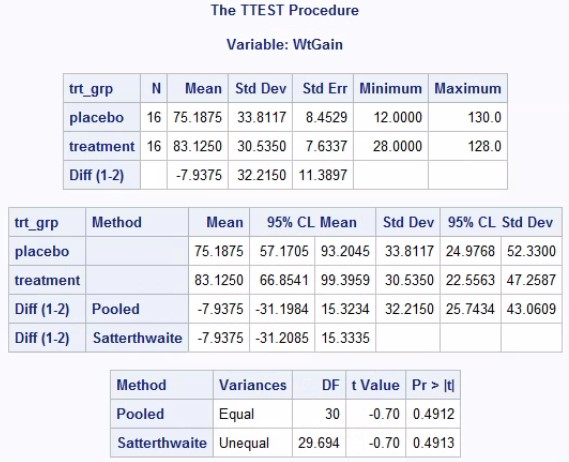
Here the t-value is –0.70, degrees of freedom is 30 and P value is 0.4912 which is greater than 0.05, so we accept the null hypothesis that there is no evidence of a significant difference between the means of treatment groups. The mean in placebo group is 75.1875 and mean in Treatment group is 83.1250. The mean difference the treatment groups (Treatment-Placebo) is –7.9375 and the 95% CI for the mean difference is [–31.1984, 15.3234]. The 95% confidence interval includes a treatment difference of 0, which supports the conclusion that the data fail to provide any evidence of a difference between the treatment groups.
Model Checking
Note: Before entering straight into the t-test we need to check whether the assumptions (like the equality of variance, the observations should be independent, observations should be normally distributed) are met or not. If normality is not satisfied, we may consider using a suitable non-parametric test.
- Normality: You can check for data to be normally distributed by plotting a histogram of the data by treatment. Alternatively, you can use the Shapiro-Wilk test or the Kolmogorov-Smirnov test. If the test is <0.05 and your sample is quite small then this suggests you should not use the t-test. However, if your sample in each treatment group is large (say >30 in each group), then you do not need to rely so heavily on the assumption that the data have an underlying normal distribution in order to apply the two-sample t-test. This is where plotting the data using histograms can help to support investigation into the normality assumption. We have checked the normality of the observations using the code below. Here for both the treatment groups we have P value greater than 0.05 (Shapiro-Wilk test is used), therefore the normality assumption is there for our data.
proc univariate data=d1 normal;
qqplot WtGain;
by trt_grp;
run; Output:
Figure 2: The results of normality test for Treatment group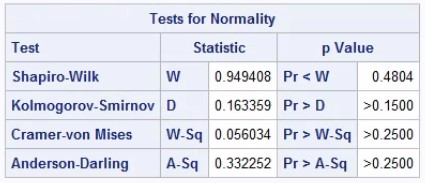
Figure 3: The results of normality test for Placebo group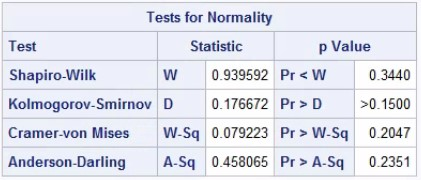
- Homogeneity of variance (or Equality of variance): Homogeniety of variance will be tested by default in PROC TTEST itself by Folded F-test. In our case the P values is 0.6981 which is greater than 0.05. So we accept the null hypothesis of F-test, i.e. variances are same. Then we will consider the pooled method for t-test. If the F test is statistically significant (p<0.05), then the pooled t-test may give erroneous results. In this instance, if it is believed that the population variances may truly differ, then the Satterthwaite (unequal variances) analysis results should be used. These are provided in the SAS output alongside the Pooled results as default.
Output:
Figure 4: Folded F-test result in PROC TTEST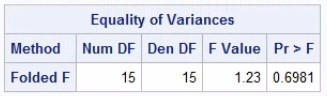
Example with unequal variances
For this example, it is important to use the Welch’s t-test (the Satterthwaite approximation is used to calculate the effective degrees of freedom and variance) results.
data d2;
length trt_grp $ 9;
input trt_grp $ WtGain @@;
datalines;
placebo 14 placebo 15 placebo 15 placebo 15
placebo 16 placebo 18 placebo 22 placebo 23
placebo 24 placebo 25 placebo 25
treatment 10 treatment 12 treatment 14 treatment 15
treatment 18 treatment 22 treatment 24 treatment 27
treatment 31 treatment 33 treatment 34 treatment 34
treatment 34
;
run;
proc ttest data=d2;
class trt_grp;
var WtGain;
run;Output:
Figure 1: Test results for independent t-test using PROC TTEST in SAS